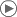Synonyymit
| Kieli | Käännökset |
|---|---|
| espanja | espacio vectorial |
| italia | spazio vettoriale |
| japani | ベクトル空間 (bekutoru kūkan) |
| kreikka | διανυσματικός χώρος (dianysmatikós chóros) |
| portugali | espaço vetorial |
| puola | przestrzeń wektorowa, przestrzeń liniowa |
| ranska | espace vectoriel |
| ruotsi | vektorrum, linjärt rum |
| saksa | Vektorraum |
| suomi | vektoriavaruus |
| tanska | vektorrum |
| tšekki | vektorový prostor |
| unkari | vektortér |
| venäjä | ве́кторное простра́нство (véktornoje prostránstvo) |
Määritelmät
Substantiivi
- (algebra, geometry, topology) A set of elements called vectors, together with some field and operations called addition (mapping two vectors to a vector) and scalar multiplication (mapping a vector and an element in the field to a vector), satisfying a list of constraints; equivalently, a module over a field.
Esimerkit
- A vector space is a set of vectors which can be linearly combined.
- Each vector space has a basis and dimension.
Taivutusmuodot
| Monikko | vector spaces |
(algebra, geometry, topology) A set of elements called vectors, together with some field and operations called addition (mapping two vectors to a vector) and scalar multiplication (mapping a vector and an element in the field to a vector), satisfying a list of constraints; equivalently, a module over a field.
Vector addition and scalar multiplication: a vector v (blue) is added to another vector w (red, upper illustration). Below, w is stretched by a factor of 2, yielding the sum v + 2w.
(algebra, geometry, topology) A set of elements called vectors, together with some field and operations called addition (mapping two vectors to a vector) and scalar multiplication (mapping a vector and an element in the field to a vector), satisfying a list of constraints; equivalently, a module over a field.
A vector v in R2 (blue) expressed in terms of different bases: using the standard basis of R2: v = xe1 + ye2 (black), and using a different, non-orthogonal basis: v = f1 + f2 (red).
(algebra, geometry, topology) A set of elements called vectors, together with some field and operations called addition (mapping two vectors to a vector) and scalar multiplication (mapping a vector and an element in the field to a vector), satisfying a list of constraints; equivalently, a module over a field.
Vector addition: the sum v + w (black) of the vectors v (blue) and w (red) is shown.