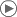Sanakirja.org

(geometry) The irrational number (approximately 1.618), usually denoted by the Greek letter φ (phi), which is equal to the sum of its own reciprocal and 1, or, equivalently, is the square root of the sum of itself and 1.

The golden ratio (phi) represented as a line divided into two segments a and b, such that the entire line is to the longer a segment as the a segment is to the shorter b segment.

(geometry) The irrational number (approximately 1.618), usually denoted by the Greek letter φ (phi), which is equal to the sum of its own reciprocal and 1, or, equivalently, is the square root of the sum of itself and 1.

A golden rectangle with long side a + b and short side a can be divided into two pieces: a similar golden rectangle (shaded red, right) with long side a and short side b and a square (shaded blue, left) with sides of length a. This illustrates the relationship ⁠a + b/a⁠ = ⁠a/b⁠ = φ.

(geometry) The irrational number (approximately 1.618), usually denoted by the Greek letter φ (phi), which is equal to the sum of its own reciprocal and 1, or, equivalently, is the square root of the sum of itself and 1.

If φ were rational, then it would be the ratio of sides of a rectangle with integer sides (the rectangle comprising the entire diagram). But it would also be a ratio of integer sides of the smaller rectangle (the rightmost portion of the diagram) obtained by deleting a square. The sequence of decreasing integer side lengths formed by deleting squares cannot be continued indefinitely because the positive integers have a lower bound, so φ cannot be rational.