Ääntäminen
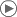 US:
US:- IPA: /spɪnɔɹ/
| Kieli | Käännökset |
|---|---|
| hollanti | spinor |
| italia | spinore |
| ranska | spinoriel, spineur |
| venäjä | спино́р (spinór) |
Määritelmät
Substantiivi
- (algebra) An element of the fundamental representation of a Clifford algebra that transforms to its negative when the space is rotated through a complete turn from 0° to 360°.
Taivutusmuodot
| Monikko | spinors |
Luokat
(algebra) An element of the fundamental representation of a Clifford algebra that transforms to its negative when the space is rotated through a complete turn from 0° to 360°.

A spinor visualized as a vector pointing along the Möbius band, exhibiting a sign inversion when the circle (the "physical system") is continuously rotated through a full turn of 360°.
(algebra) An element of the fundamental representation of a Clifford algebra that transforms to its negative when the space is rotated through a complete turn from 0° to 360°.
A gradual rotation can be visualized as a ribbon in space. Two gradual rotations with different classes, one through 360° and one through 720° are illustrated here in the belt trick puzzle. A solution of the puzzle is a continuous manipulation of the belt, fixing the endpoints, that untwists it. This is impossible with the 360° rotation, but possible with the 720° rotation. A solution, shown in the second animation, gives an explicit homotopy in the rotation group between the 720° rotation and the 0° identity rotation.
(algebra) An element of the fundamental representation of a Clifford algebra that transforms to its negative when the space is rotated through a complete turn from 0° to 360°.
The spin representation Δ is a vector space equipped with a representation of the spin group that does not factor through a representation of the (special) orthogonal group. The vertical arrows depict a short exact sequence.